音響音声学とは何か
音声によるコミュニケーションにおいては、話し手と聞き手が存在します。話し手は音声器官を動かすことで音声を産出します。一方、聞き手は音声を耳で聞き、脳で処理することで、話し手が言っていることを理解します。このとき、話し手と聞き手を繋ぐものは、(多くの場合)空気の振動(すなわち音響信号)です。話し手が音声器官を動かすことで空気の振動が生み出され、聞き手はそれを捉えて処理しているのです。
別の言い方をすると、音声の産出(production)とは話し手が言いたいことを音響信号に変換するプロセスであり、音声の知覚(perception)とは聞き手が音響信号を感知しそこから音声・音韻にかかわる情報を解読するプロセスだということができます。
音響音声学(acoustic phonetics)は、音声の音響信号としての側面を分析する(音響分析をする)分野です。こんにちの音響音声学ではたいてい、マイクで音声を録音した上で、コンピュータ上で音響分析をします。
音響音声学のメリットは、音声を客観的に分析できる点にあります。例えば、ある母音が [i] に近いか [e] に近いかというのは、伝統的な調音音声学ではもっぱら聴覚印象に頼っていました(母音の解説参照)。これに対し音響音声学では、後で学習するフォルマントという音響指標によって定量的に分析をします。もちろん、音声の客観的な分析は音響音声学に限ったものではありません。X線撮影やMRIによる調音運動観測も、客観的な音声の分析手法の一種です。なお、調音運動観測は音声の産出の過程を捉えるものであり、音響分析は産出の出力形を分析するものなので、そもそも捉えるレベルが異なるという点には注意が必要です。
音響音声学のもう一つのメリット――より現実的なメリット――としては、安価に行えるということがあります。上に述べた調音運動観測は高価な装置が必要です。音響分析も、かつては大きくて高価な装置で行われていた時代がありました。しかし今日ではコンピュータ上で行うことが一般的になり、ソフトウェアもどんどん安価になり、ついには高機能のフリーソフトが出てきました。分析のためのコストは、一昔前と比べてかなり下がったのです。音声の音響分析は、知識とスキルさえきちんと身に着ければ、誰でも手軽に行うことができようになったといっても過言ではありません。
さて、音響音声学は上に述べたように、音声の音響信号としての側面を捉えるものです。そこで必要となる知識には、音声に限らない音・音響信号全般に関する部分と、音声に特有の部分とがあります。以下の解説では、まずは音全般に関するところから見ていき、徐々に音声に特有の部分を見ていくことになります。
音とは何か
音声は音(オト)の一種ですが、音とは何でしょうか。日本音響学会編(2003: 38)では次のように定義されています。
音 sound
音波(弾性波)またはそれによって起こされる聴覚的感覚(音感覚ともいう)。すべての音波(弾性波)が聴覚的感覚を引き起こすとは限らない。例えば超音波周波数の音。音の存在する媒質を付けていうことがある。例えば、空中音、水中音、固体音。
日本音響学会編(2003: 38)
上の最初の文からもわかるように、音は物理的に音波と同義のものとして定義されることもあれば、聴覚的に定義されることもあります。聴覚的な定義に従うならば、人間の聴覚器官で捉えられないものは音ではないことになります。
さて、上では音波(弾性波)がキーワードになっています。では、音波(弾性波)とは何でしょうか?日本音響学会編(2003: 232)では、弾性波を次のように定義しています。
弾性波 elastic wave
弾性媒質中における、応力、粒子変位、粒子速度などの振動およびこれらの振動の伝搬現象。空気中の音波は縦波である。
日本音響学会編(2003: 232)
例えば、私たちが木琴をたたくとします。そうすると木琴の板は振動します。この木琴の振動は、その周辺にある空気に伝わり、空気が振動することになります。この空気が、上で媒質と言っているものに当たります。(音の媒質は必ずしも空気であるとは限りませんが、音響音声学ではたいてい、媒質として空気を想定しています。)そして、木琴の周辺の空気から離れたところの空気へと、振動が次から次へ伝わっていきます。つまり、振動が伝搬されていくのです。そして私たちの耳のまわりの空気が振動し、私たちの耳の鼓膜が振動することになります。そこから先どうなっていくかはまた、「聴覚と音声知覚」を学習する際に学びます。
上の引用の最後に書かれていた「空気中の音波は縦波である」というのも、重要なポイントです。世の中には様々な波がありますが、それらは縦波(longitudinal wave)と横波(transverse wave)に分類することができます。縦波は進行方向に振動する波であり、横波は進行方向と垂直の方向に振動する波です。音波は縦波という特徴を持っています。

(Christophe Dang Ngoc Chan (cdang), CC BY-SA 3.0 http://creativecommons.org/licenses/by-sa/3.0/, via Wikimedia Commons)
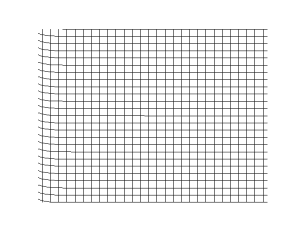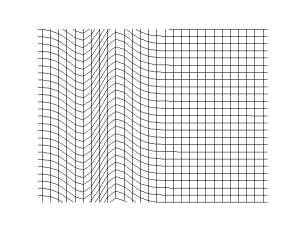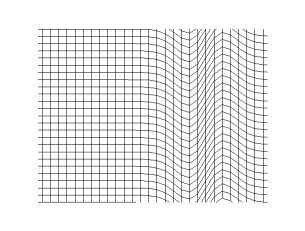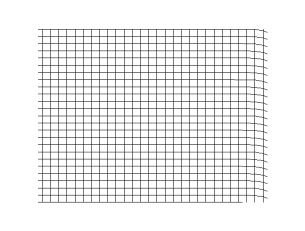
(Christophe Dang Ngoc Chan (cdang), CC BY-SA 3.0 http://creativecommons.org/licenses/by-sa/3.0/, via Wikimedia Commons)
参考動画
音の波形
どのような波であれ、図として表すことができます。波を図にするときには、横軸に時間をとり、縦軸に振幅をとることが一般的です。音の場合、空気圧が振幅に相当します。上で音は縦波であると書きましたが、図にすると横波のような見え方になります。
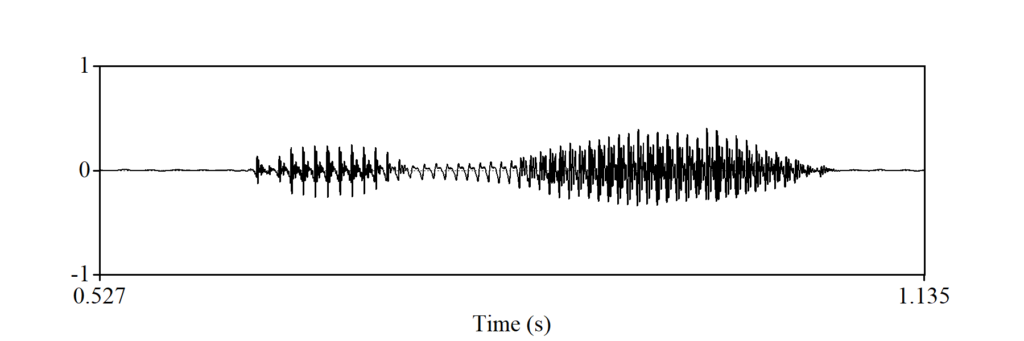
周期波と非周期波
音(音波)は(あるいは、音波に限らずいかなる波も)周期波(periodic wave)と非周期波(aperiodic wave)に分けることができます。周期波は文字通り、一定のパターンが繰り返される波のことです。それに対し非周期波は、一定のパターンの繰り返しではない波のことです。以下の三つの図に示される波は、周期波でしょうか?非周期波でしょうか?
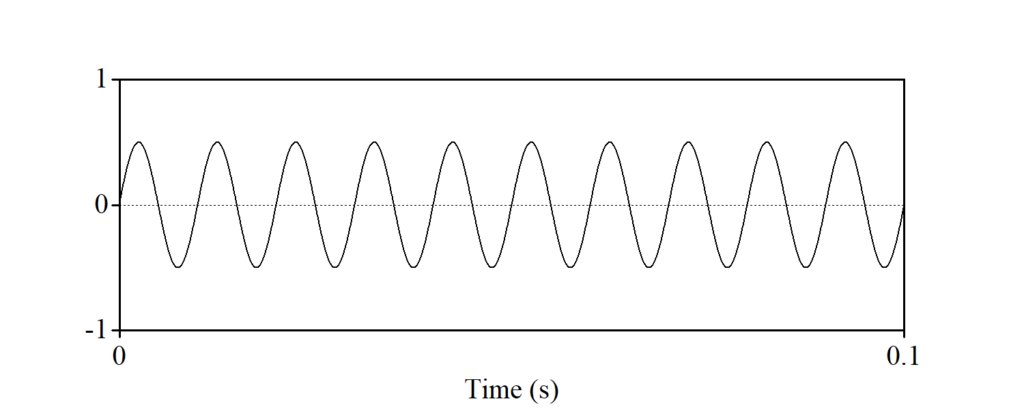
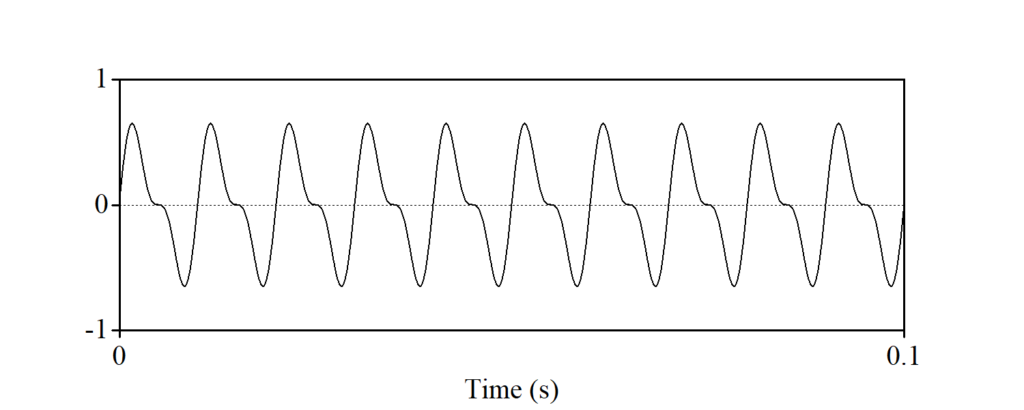
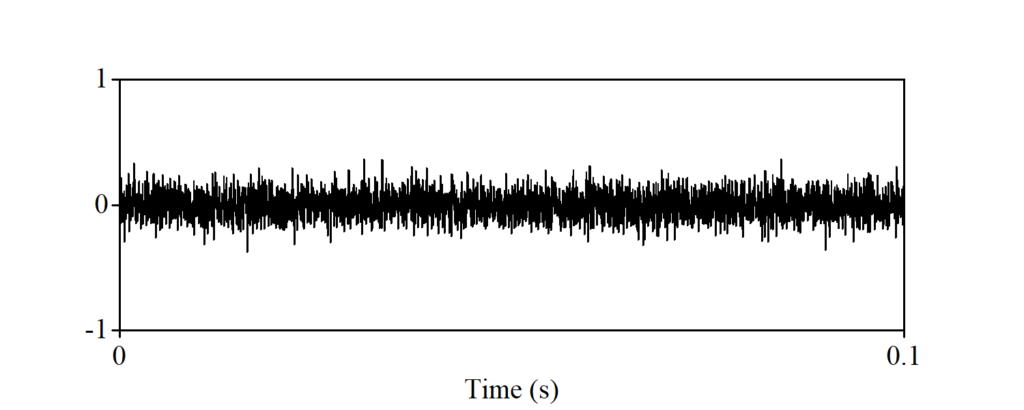
aは周期波です。bはaとパターンが異なりますが、これも周期波です。それに対し、cは非周期波で、一定のパターンを見出すことができません。
音響音声学にひきつけて少しだけ述べておくと、音声の興味深いところは、周期波っぽいもの(厳密な意味で完全な周期波とは言えないものの、それに近い特徴を持ったもの)と、非周期波の両方が含まれる点にあります。例えば、前者の典型が母音で、後者の典型が無声摩擦音です。
正弦波
波を理解する上で、正弦波の理解が重要となります。正弦というのは、数学の三角関数で習う「サイン・コサイン・タンジェント」の「サイン」(sine)のことです。例えば、時間を t とした以下の数式を見てみましょう。
![]()
この数式を図にすると、以下のようになります。
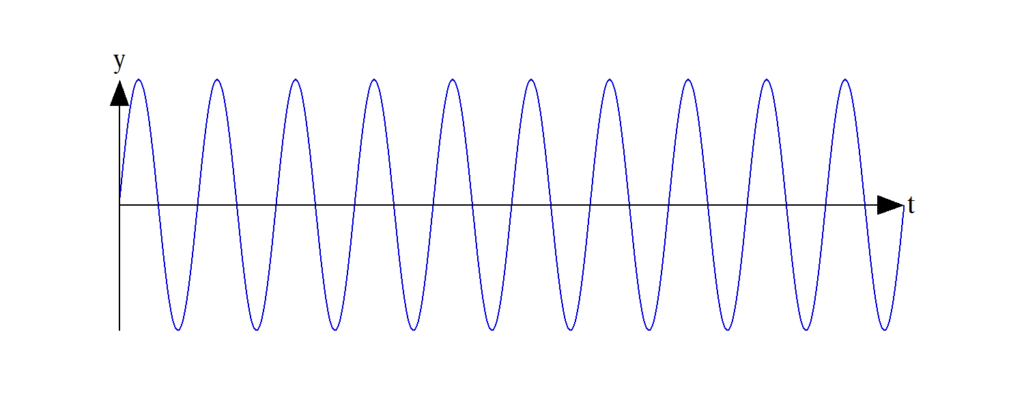
正弦波には様々なバリエーションがあります。以下の四つのグラフは何が異なるでしょうか?
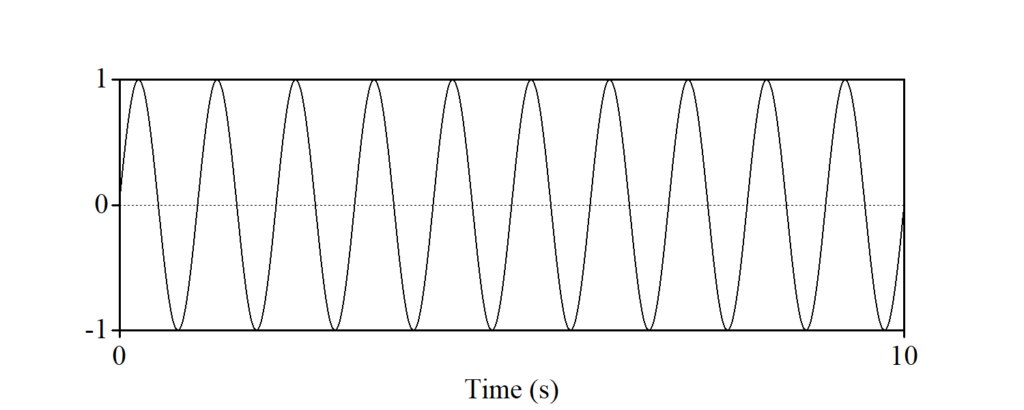
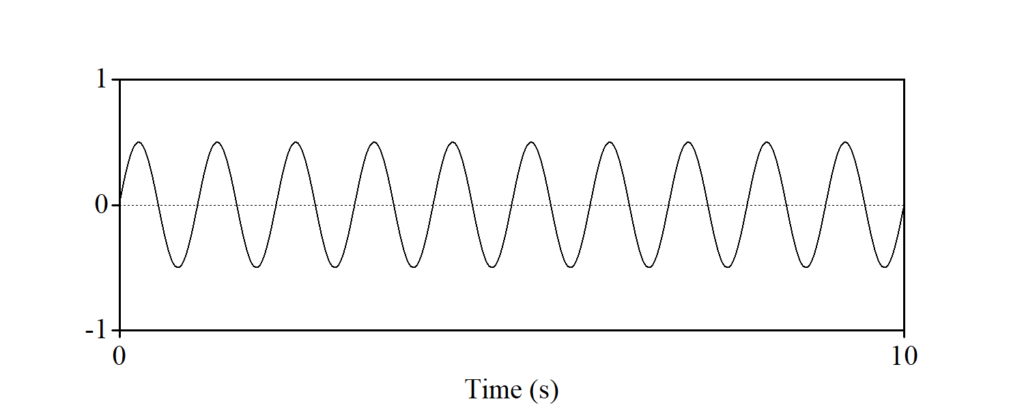
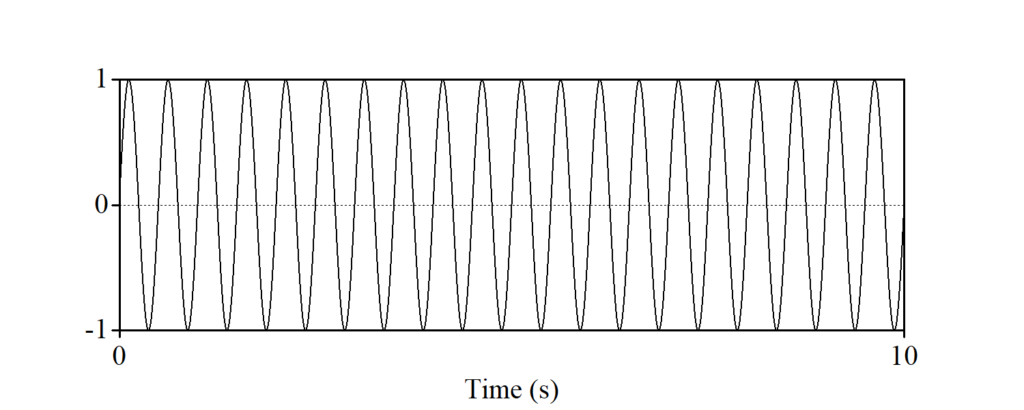
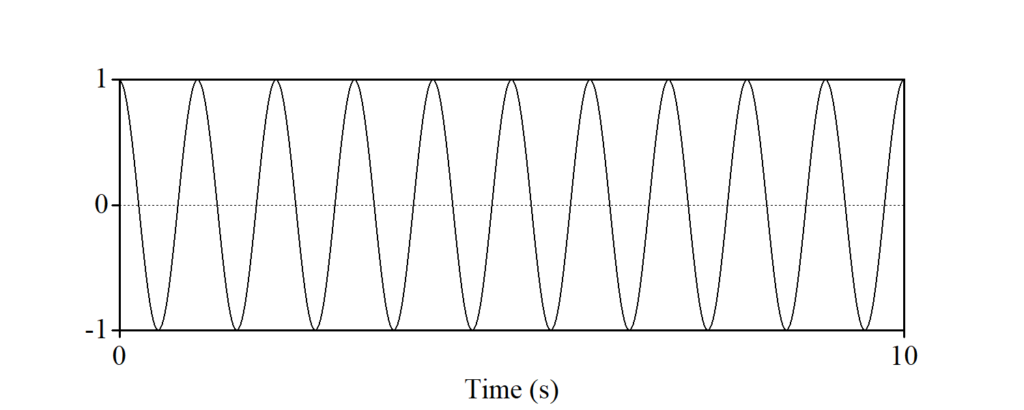
正弦波aを基準と見ていきましょう。正弦波bは、グラフで見ると上下方向のふれ幅が半分になっています。専門的な言い方をすると、「(最大)振幅」((peak) amplitude)が半分になっています。正弦波cは、繰り返しのパターンが半分になり、一定時間当たりの繰り返しの数が倍になっています。専門的な言い方をすると、「周期」(period)が半分になっている、もしくは「周波数」(frequency)が倍になっていると言うことができます。正弦波dは、横軸(t)が0の時点で縦軸(y)が1であり、先の図とは横方向に少しずれています。専門的な言い方をすると、「位相」(phase)が異なるということができます。
音声を扱う上では最後の位相は問題にならないことが多いので、ここから先は振幅と周期/周波数のみを見ていきます。以下の図は、横軸を時間とした正弦波における振幅と周期(period)を示しています。
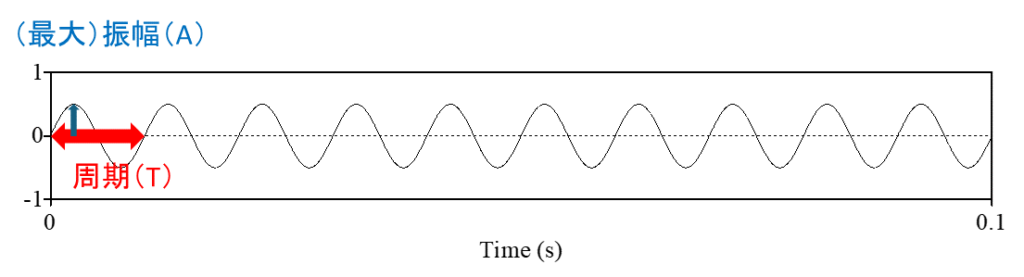
周波数は周期が単位時間あたり(ここでは1秒あたり)何回繰り返すかで、周期の逆数(つまり、1から割った数)になります。周波数の単位は Hz(Hertz、ヘルツ)です。周期(T)と周波数(f)の関係は以下の式で表せます。
![]()
さて、振幅(A)・周期(T)の異なる正弦波を数式で表現すると、次のようになります。
![]()
周期のかわりに周波数(f)を用いれば、次のようになります。
![]()
なぜこういう式になるかは、三角関数を理解している人であればわかると思いますが、三角関数を忘れてしまった人は、とりあえず最後の式だけは覚えておきましょう。 正弦波としてあらわれる音は、純音(pure tone)といいます。身近なところでは、音叉の音や時報の音が純音です。純音は周波数が高いほど高い音として聞こえます。
スペクトル
正弦波は足し合わせることができます。例えば、振幅と周波数の異なる以下の二つの正弦波を足し合わせると、どうなるでしょうか?
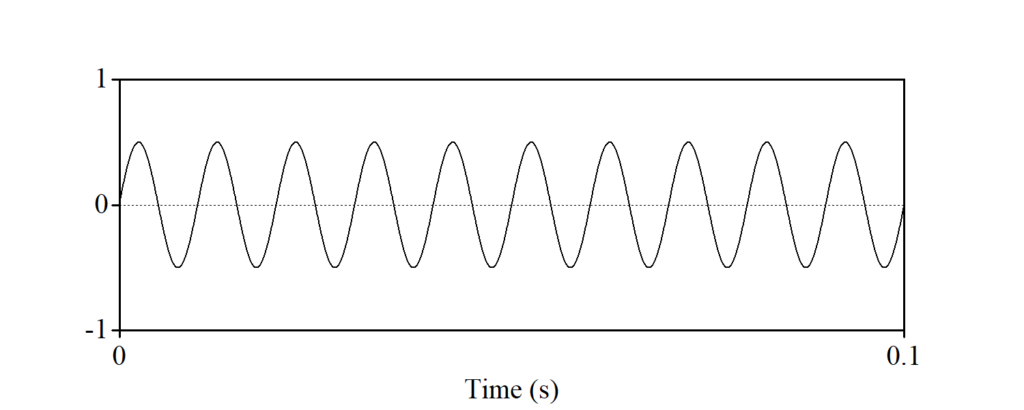
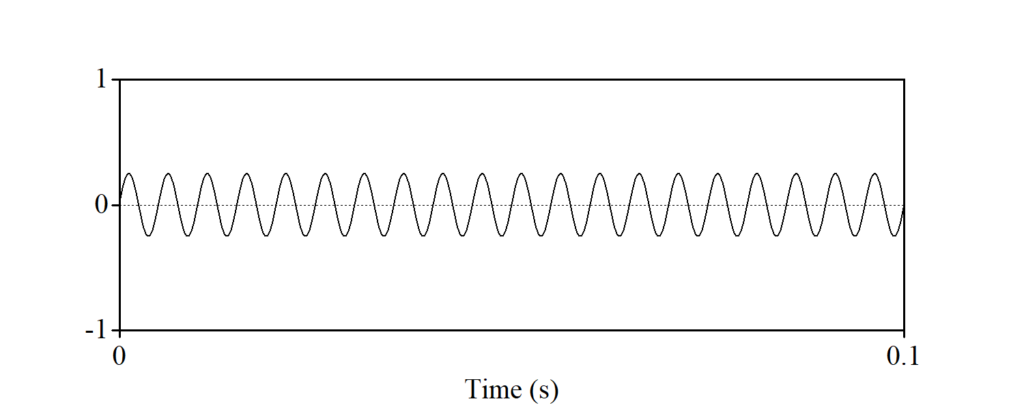
足し合わせた波は、下の図のようになります。
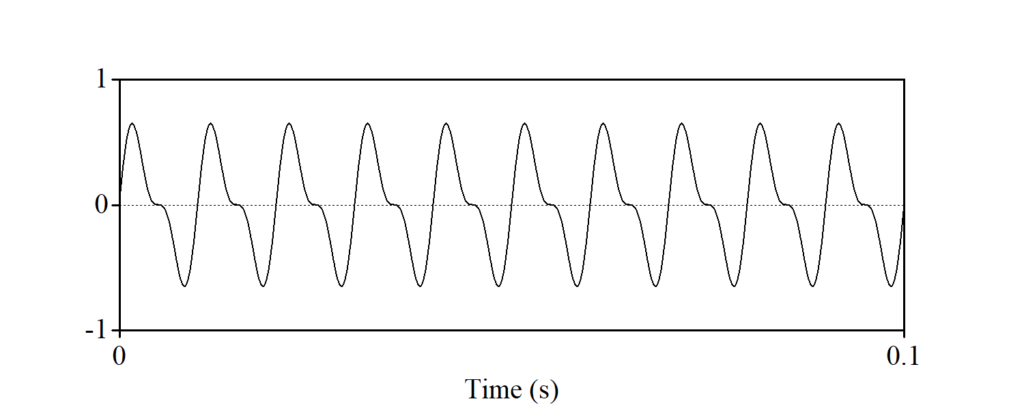
波は足し合わせることができるだけでなく、正弦波に分解することができます。(a) と (b) を足して (c) を作るというプロセスを反対にし、(c) を (a) と (b) に分解するということです。あらゆる周期波は、ある周波数の正弦波と、その整数倍の(複数の)正弦波に分解することができます。例えば (c) の場合、100 Hz の正弦波と、その2倍である 200 Hz の正弦波に分解されます。もっと複雑な周期波になれば、例えば 100 Hz、200 Hz、300 Hz、400 Hz … の正弦波に分解される――といった具合に、たくさんの成分に分解されることになります。そして、それらの成分は必ず、ある周波数の整数倍になっているのです。
実は、正弦波に分解できるのは周期波に限りません。非周期波も正弦波に分解することができます。ということは、あらゆる波は正弦波に分解できるということになります。ただし、非周期波の場合、ある周波数の整数倍の成分に分解されるというのではなく、無限の中間段階をもった成分に分解されます。なお、この分解は、数学において「フーリエ変換」(Fourier transform)と呼ばれます。
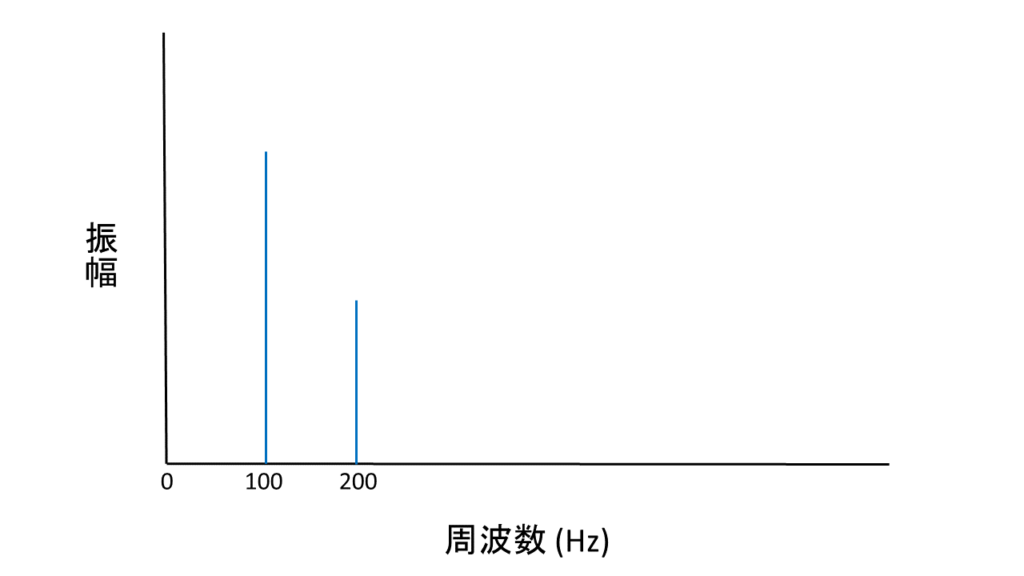
さて、このようにして分解して各成分を示した図を「スペクトル」(spectrum)といいます。別の言い方をすると、スペクトルとは、信号を構成する周波数成分を表した図ということができます。音声研究においては一般に、音を純音(正弦波)に分解し、横軸を周波数、縦軸を振幅としてあらわす。例えば、上の (c) をスペクトルにすると下の図のようになります。
サウンド・スペクトログラム
音声においては、同じ音がずっと流れ続けることはなく、刻一刻と音の特徴が変化します。そこでその変化を捉えるため、瞬間瞬間の音の特徴とその時間変化をみることが重要になります。そこで、「サウンド・スペクトログラム」(sound spectrogram)(あるいは単に「スペクトログラム」ともいいます)が利用されます。次の図は、ある単語の音声波形とサウンド・スペクトログラムを並べて示したものです。
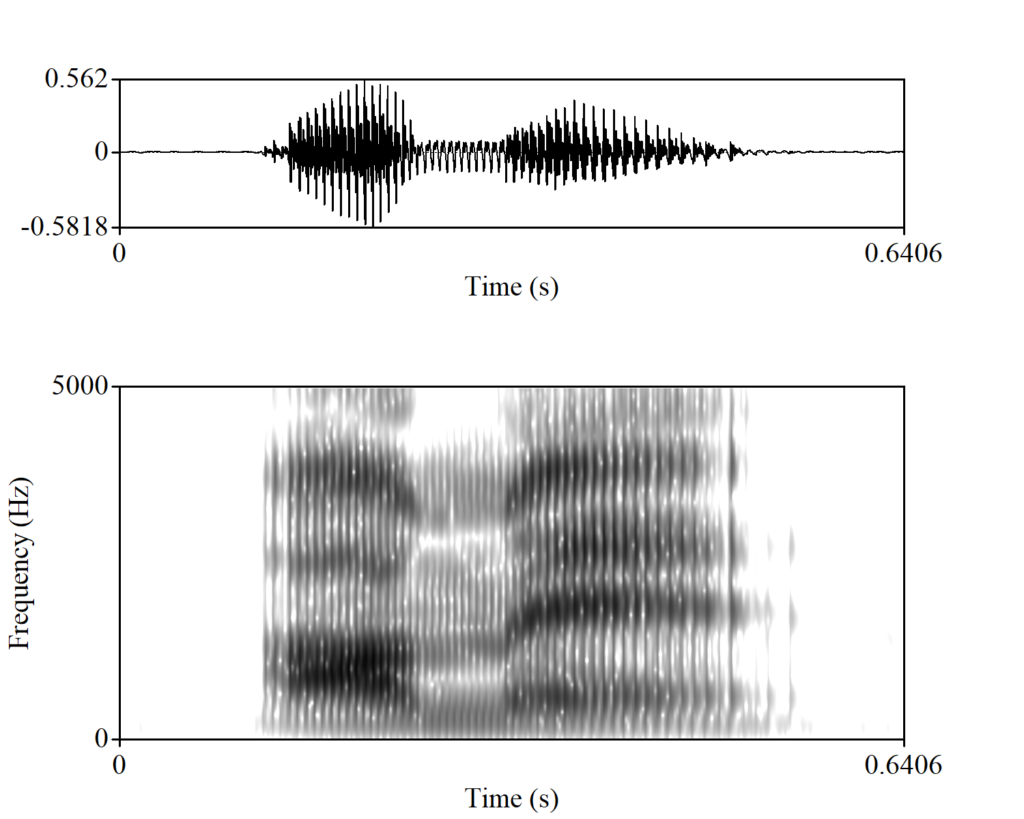
皆さんはもしかしたら、メディアで容疑者の声紋鑑定をするような場面で、このような図を見たことがあるかもしれません。サウンド・スペクトログラムは、確かに科学的な犯罪捜査において用いられることがあるようですが、言語学的関心にもとづく音響音声学においてもよく用いられるものです。
スペクトルは一般に、周波数を横軸に、振幅を縦軸にとって示します。これに対してサウンド・スペクトログラムは、周波数を縦軸にとり、振幅を濃淡によってあらわすことが一般的です。そして、スペクトルにはなかかった「時間」という情報が加わり、これが横軸に示されます。(なお、モノクロではなくカラーや立体のサウンド・スペクトログラムもあり、その場合は振幅が違ったかたちで表現されます。)サウンド・スペクトログラムは、音声を非常に短い時間幅で切り分け、各時間幅においてフーリエ変換をしてスペクトルを生成し、時間軸にしたがって並べたものだと理解すればよいでしょう。
学習案内
斎藤純男 (2006) 『日本語音声学入門 改訂版』 三省堂. [第10章.] [Amazonリンク]
[第10章]
川原繁人(2018)『ビジュアル音声学』三省堂.[Amazonリンク]
[3.1~3.2において、数学的なところから文系学生にもわかりやすいように説明されています。]
ラディフォギッド, P. (1999) 『音声学概説』 大修館書店. [Amazonリンク]
[第8章]
ローレンス, J.R. 他 (2008) 『新ことばの科学入門 第2版』 医学書院. [Amazonリンク]
[第3章.]
Johnson, K. (2011) Acoustic and auditory phonetics, 3rd edition. Chichester: Wiley-Blackwell. [Amazonリンク]
[音響音声学をメインとした教科書で、Chapter 1で音響音声学の基礎が詳しく説明されています。]
参照文献
日本音響学会 編 (2003) 『新版音響用語辞典』コロナ社. [Amazonリンク]